Tree Data Structure
Binary Search Tree
The word binary indicates that each nodes has at most 2 children. It's called a search tree because the order of the nodes is sorted by the value of the data. Let's take a look at an example:
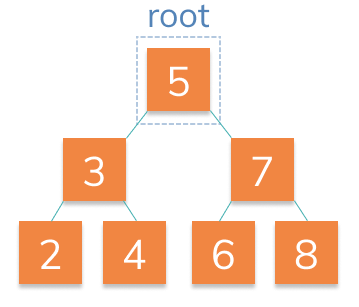
Any child that is to the left of it's parent is smaller. Any child that is to the right of it's parent is greater. For example, the root 5 has two children 3 and 7. Since 3 is less than 5, it is to the left of 5.
Knowing that the data is in this order, it will take us less time to find a particular node. We can look for 4. Starting at the root, we know it's less than 5 so we go left. We encounter 3 next and know that 4 is greater than 3, so we go right. There, we find 4. On average this will be faster than searching randomly. The time savings become greater the bigger the tree is.
Merkle Trees
Quite simply, a Merkle Tree is a data structure that allows us to make efficient verifications that data belongs in a larger set of data.
They are commonly used in Peer to Peer networks where efficient proofs of this nature will help increase the scalability of the network.
ABCDEFGH <-- Merkle Root
/ \
ABCD EFGH
/ \ / \
AB CD EF GH
/ \ / \ / \ / \
A B C D E F G H
Each single letter represents a hash. The combined letters represent concatenated hashes that have been combined and hashed to form a new hash.
As peers in a system, I can simply ask if your root matches mine. If so, we agree. This is a nice optimization for distributed systems of any kind!
This binary tree structure affords us one further optimization: it allows us to verify a single piece of data belongs in the tree without having all of the data.
ABCDEFGH
/ \
ABCD EFGH
/ \ / \
- - EF GH
/ \ / \ / \ / \
- - - - E F - -
What do we need in order to prove that E belongs in this tree?
Just F, GH, ABCD. We use these to calculate EF, EFGH, and ABCDEFGH. Then we can compare the result to our expected root ABCDEFGH.
If something went wrong along the way, we would notice it at the root. For example if we replaced E with M:
ABCDMFGH
/ \
ABCD MFGH
/ \ / \
- - MF GH
/ \ / \ / \ / \
- - - - M F - -
We can quickly check ABCDMFGH against the our expected root ABCDEFGH and see we did not get our expected hash. Something's wrong.
The savings become important with larger trees where the average case for verification of tree is log2(n) where n is the number of nodes in the tree. So for a tree of size 128, it would take only 7 hashes to determine the root.